 De: La Frikipedia, la enciclopedia extremadamente seria.
De: La Frikipedia, la enciclopedia extremadamente seria. De: La Frikipedia, la enciclopedia extremadamente seria.
De: La Frikipedia, la enciclopedia extremadamente seria.

|
ATENCIÓN Este artículo es un truño, es sólo un esbozo de un artículo o es demasiado corto o el que lo ha escrito se cree que esto es un vil diccionario. Su autor puede estar bajo los efectos del alcohol o ser un inútil. Quizá haya pistas en la discusión. ¡Mejora la Frikipedia ampliando y mejorando el artículo! |
Sea 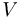 un vaso compacto y
un vaso compacto y 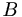 un bebedor. Sea
un bebedor. Sea  una borrachera continua. Entonces la borrachera
una borrachera continua. Entonces la borrachera 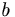 es uniformemente continua.
es uniformemente continua.
Supongamos que 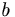 no fuese uniformemente continua. Esto implica que existe un cierto grado de embriaguez no superable
no fuese uniformemente continua. Esto implica que existe un cierto grado de embriaguez no superable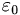 tal que para cada tiempo
tal que para cada tiempo 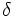 existen rellenos del vaso
existen rellenos del vaso 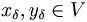 tales que
tales que 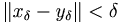 y que
y que 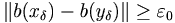 . En particular si
. En particular si 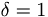 se tiene que existen
se tiene que existen 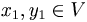 tales que
tales que 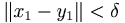 y que
y que 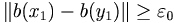 . Si
. Si 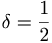 se tiene que existen
se tiene que existen 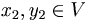 tales que
tales que  y que
y que 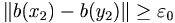 . Si
. Si 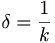 se tiene que existen
se tiene que existen 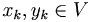 tales que
tales que 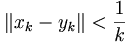 y que
y que 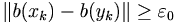 . Podemos entonces construir sendas sucesiones de rellenos del vaso
. Podemos entonces construir sendas sucesiones de rellenos del vaso 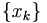 ,
, 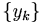 . Como el vaso es compacto, tenemos que existen sendas subusucesiones convergentes de rellenos de vasos con identico límite ya que
. Como el vaso es compacto, tenemos que existen sendas subusucesiones convergentes de rellenos de vasos con identico límite ya que 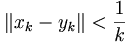 . Por tanto tenemos que las sucesiones de borracheras
. Por tanto tenemos que las sucesiones de borracheras 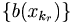
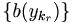 tienen idéntico límite por la continuidad de la borrachera lo cual es imposible ya que habíamos supuesto la existencia de un grado de embriaguez no superable.
tienen idéntico límite por la continuidad de la borrachera lo cual es imposible ya que habíamos supuesto la existencia de un grado de embriaguez no superable.
Este teorema tiene consecuencias habitualmente apreciadas en toda fiesta. ¡Cerveza para todos! ¡Alcohol sin fin! Normalmente su aplicación conlleva disfunción de la apreciación del atractivo físico del sexo opuesto y puede concluir en finales inesperados nocturnos en lugares desconocidos y/o con desconocidos.
Autor(es):